신장트리

신장 트리란 그래프 상에서 모든 노드가 사이클 없이 연결된 부분 그래프를 뜻한다.
하나의 그래프에는 신장 트리가 많이 존재할 수 있다.
단, 그래프의 모든 정점을 포함 해야한다.
최소 신장 트리
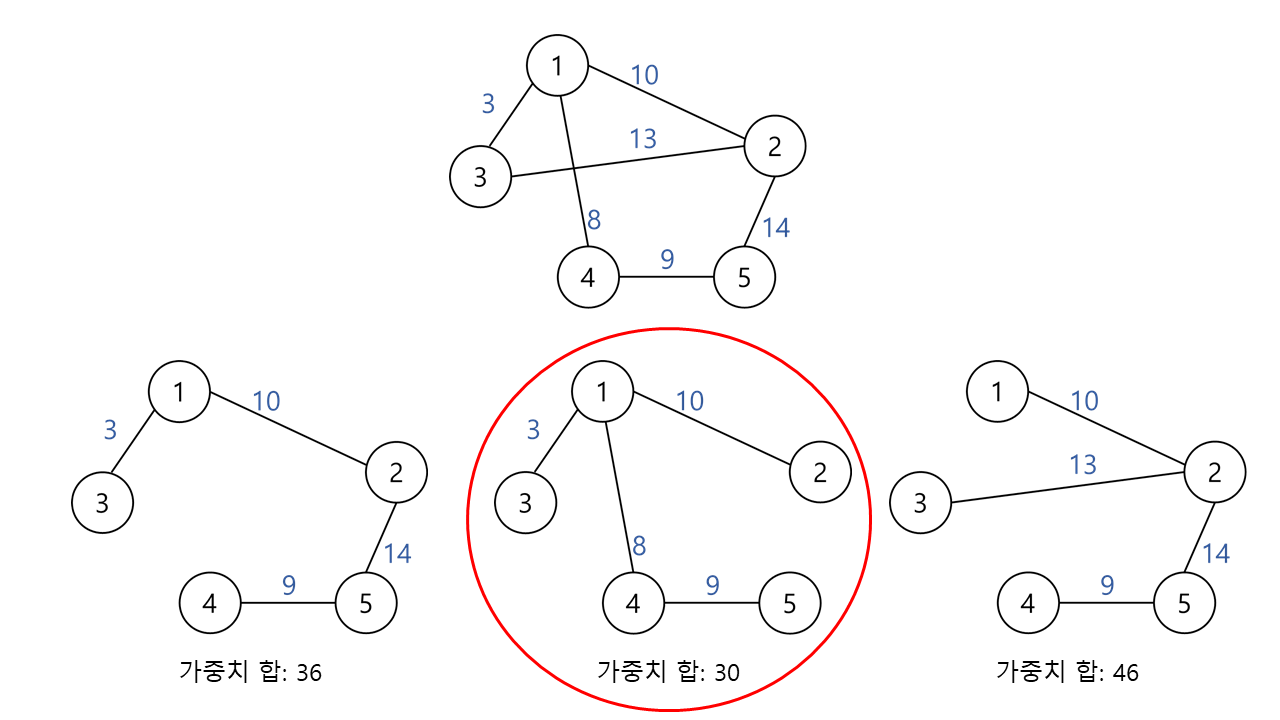
최소신장트리는 신장 트리중 간선의 가중치 합이 가장 작은 트리를 말한다.
알고리즘 문제에서 유용하게 사용될 수 있다.
ex)
- 섬 연결하기 (프로그래머스)
- 전력망을 둘로 나누기 (프로그래머스)
- 별자리 만들기 (백준 4386)
- 네트워크 연결 (백준 1922)
- 도시 분할 계획 (백준 1647)
최소 신장 트리 구현
최소 신장 트리 구현의 대표적인 알고리즘은 크루스칼 알고리즘이다.
크루스칼 알고리즘 과정
1) 간선은 가중치를 기준으로 오름차순 정렬한다.
2) 간선을 하나씩 살핀다. 간선을 MST에 추가했을 때 MST에 사이클이 생기지 않으면 추가한다. 사이클이 생긴다면 다음 간선으로 넘어간다.
<find union을 이용한 크루스칼 알고리즘 구현 예제>
import java.util.*;
class Solution {
public int solution(int n, int[][] costs) {
int answer = 0;
int[] graph = new int[n];
boolean[] visit = new boolean[n];
for(int i=0; i<n; i++){
graph[i]=i;
}
Arrays.sort(costs,(a,b)->Integer.compare(a[2],b[2]));
for(int i=0; i<costs.length; i++){
if(find(graph, costs[i][0])!=find(graph,costs[i][1])){
unite(graph,costs[i][0],costs[i][1]);
answer+=costs[i][2];
}
}
return answer;
}
private int find(int[] graph, int x){
if(graph[x]==x){
return x;
}
return find(graph,graph[x]);
}
private void unite(int[] graph, int x, int y){
int a = find(graph,x);
int b = find(graph,y);
graph[a]=b;
}
}
'알고리즘 > 탐욕법(Greedy)' 카테고리의 다른 글
| 프로그래머스 - 섬 연결하기(Java) (1) | 2025.02.04 |
|---|---|
| 프로그래머스 - 구명보트 (1) | 2025.02.02 |
| 프로그래머스 - 큰 수 만들기(Java) (1) | 2025.02.01 |
| 프로그래머스 - 체육복(Java) (0) | 2025.01.30 |