https://school.programmers.co.kr/learn/courses/30/lessons/12914
프로그래머스
SW개발자를 위한 평가, 교육, 채용까지 Total Solution을 제공하는 개발자 성장을 위한 베이스캠프
programmers.co.kr
처음에는 재귀호출을 이용해서 가능한 모든 경우의 수를 구해줬더니 시간초과가 발생했다.
class Solution {
public static long answer = 0;
public long solution(int n) {
dp(0,n);
return answer;
}
public void dp(int sum, int n){ //총 뛴 칸,n
if(sum == n){
answer=(answer+1)%1234567;
return;
}
if(sum>n){
return;
}
for(int i=0; i<2; i++){
if(sum+(i+1)<=n){
dp(sum+(i+1),n);
}
}
}
}
이 문제에서는 가장 중요한 것은 각 위치에 도달할 수 있는 경우의 수가 피보나치 수열로 이루어져 있다는 것이다.
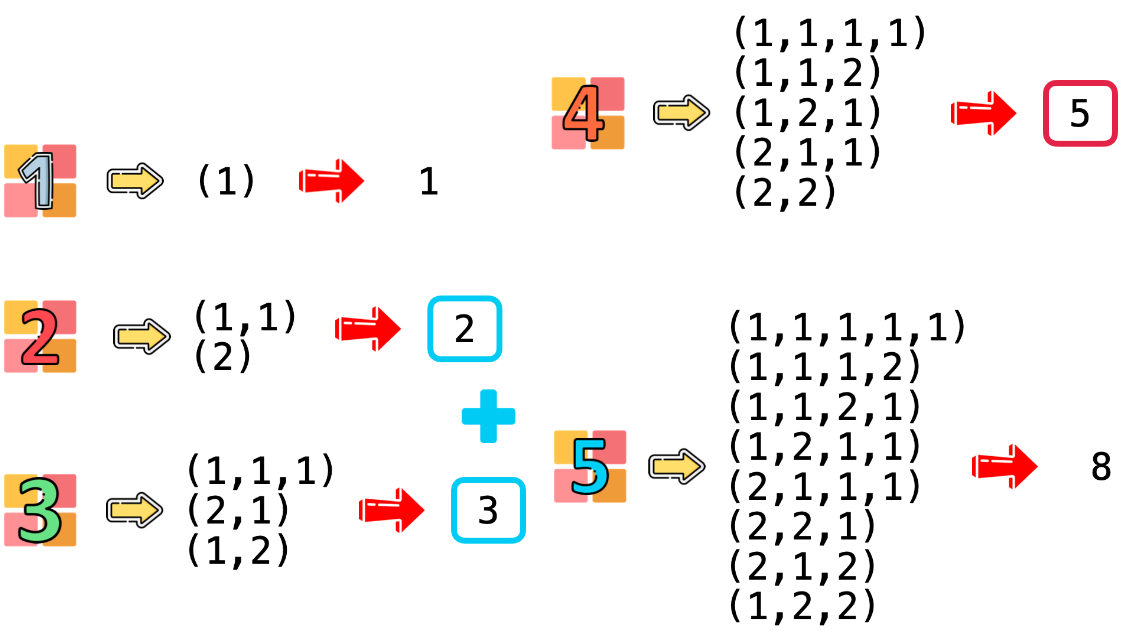
피보나치 수열을 이용하면 (현재위치 -2 경우의 수) + (현재위치 -1 경우의 수)를 해주면서 n번째까지만 반복해주면 시간복잡도 O(n)으로 문제를 해결할 수 있다!!!
<정답 코드>
class Solution {
public static long answer = 0;
public long solution(int n) {
long[] dp = new long[n+2];
dp[1]=1;
dp[2]=2;
if(n==1){
return 1;
}
if(n==2){
return 2;
}
for(int i=3; i<=n; i++){
dp[i]=(dp[i-1]+dp[i-2])%1234567;
}
return dp[n];
}
}'알고리즘 > DP' 카테고리의 다른 글
| 백준 1309번 동물원[JAVA] (4) | 2025.08.12 |
|---|---|
| 프로그래머스 - 땅따먹기[Java] (0) | 2025.02.13 |
| 프로그래머스 - 등굣길[Java] (0) | 2025.02.07 |
| 프로그래머스 - 정수 삼각형 (0) | 2025.02.05 |